Quebrar uma cifra não necessariamente quer dizer o mesmo que encontrar uma maneira de descobrir segredos recuperados através da transformação de uma cifra em texto plano. Para os acadêmicos a quebra de uma cifra significa encontrar uma fraqueza de uma cifra que pode ser explorada com complexidade menor do que a força-bruta. Por exemplo, se a força bruta requer que testemos 2256 e conseguimos encontrar alguma fraqueza na cifra que nos possibilite quebra-la com “apenas” 2250 testes, já podemos dizer que a cifra foi quebrada. Ou seja, uma quebra de cifra é apenas um atestado de que a cifra não é tão segura quanto foi assegurado pelo desenvolvedor.
A maioria das quebras consideradas bem sucedidas foram primeiramente aplicadas a uma versão mais simples das cifras, e depois – as vezes anos depois – foram extendidas para outras versões da mesma cifra.
Para quebrar uma cifra devemos adotar 3 importantes passos: identificação, quebra e configuração. O primeiro passo se refere a descobrir qual sistema de cifra foi usado. É importante ressaltar que o sistema usado pode ser um desconhecido pelo criptanalista, logo é importante que o criptanalista esteja constantemente atualizado sobre novos sistemas que possam aparecer. O preâmbulo, assim como ajuda o recipiente, pode ajudar o criptanalista a descobrir qual sistema foi usado para encriptar a mensagem. Por fim, o criptanalista deve analisar a mensagem: se ela for muito pequena, provavelmente deverá esperar por mais mensagens, caso contrário ele já dispõe de informações suficientes para iniciar a quebra da mensagem.
O segundo passo, a quebra, deve ser realizada após o analista ter conhecimento do sistema usado na encriptação da mensagem. Com essa informação ele poderá testar livros de códigos, transposições e substituições que possam quebrar a mensagem, ou então determinar as partes fixas da cifra, para assim poder confirgurar as partes variáveis e com isso iniciar os testes de quebra. Vale ressaltar que o segundo passo, a quebra, é o mais complexo, podendo levar meses que se complete essa etapa do processo.
A cifra de Júlio César, como vimos, é uma cifra de Substituição. Embora Júlio César tenha movido as letras 3 posições, ele poderia ter escolhido qualquer número de 1 a 26. Com isso, já temo uma idéia de como quebrar essa cifra: vamos escrever a cifra e sua versão deslocada de 1 a 26 posições:
Cifra:
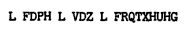
Combinações:

Assim, podemos ver que a única mensagem inteligível gerada a partir das combinações é a obtida quando movemos as letras 23 posições. Porém, assumir que as combinações irão gerar apenas 1 mensagem aceitável é razoável apenas para mensagem com mais de 5 letras aproximadamente, para cifras menores que essas podemos ter redundância nesse quesito:
Cifra:
DSP
Combinações:
| 2 | F | U | R |
| 15 | S | H | E |
Uma cifra de substituição um pouco mais complexa, mas ainda assim simples, pode ser obtida substituindo cada letra pela sua correspondente em um alfabeto “misturado”.
| A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z |
| Y | M | I | H | B | A | W | C | X | V | D | N | O | J | K | U | Q | P | R | T | F | E | L | G | Z | S |
Outro ponto relevante é que, na cifra de Júlio César, as palavras estão delimitadas por espaços, o que não acontece nas cifras de substituição usuais. Os espaços podem ser eliminados, fazendo com que o analista desconheça o número de palavras contidas na mensagem, porém o o destinatário deverá inserir espaços nos locais que ele considerar apropriado, o que pode trazer ambiguidade. Outra maneira de eliminar os espaços, e mais frequente, é usar uma letra pouco frequente do alfabeto para substitui-los, como o “X”:
| C | O | M | E | X | A | T | X | O | N | C | E |
| I | K | O | B | G | Y | T | G | K | J | I | B |
Um fato curioso a ser apontado no alfabeto apontado acima é que as letras T e Q são substituídas por elas mesmas, o que muitos estudiosos sugerem evitar. Mas segundo as estatísticas, um alfabeto gerado randomicamente tem chance de 63% de ter pelo menos uma letra repetida. Com isso, se uma ou duas letras se repetirem, a cifra ainda continuará forte o suficiente.
Para quebrar uma cifra de substituição sem considerar a força bruta (complexidade fatorial!) devemos seguir alguns passos. O primeiro consiste em contar quantas vezes cada letra aparece e representar esses dados em um mapa de frequência. Em seguida, devemos descobrir qual caractere representa o espaço (15% a 20% do conteúdo de uma mesangem considerada longa são espaços, com isso, provavelmente, a letra que tiver a maior frequência será a representação do espaço). Agora, devemos reescrever o texto com os espaços que encontramos, com isso podemos ver as palavras que possuem letras repetidas. Após isso, podemos tentar descobrir quais letras representam as vogais (onde apenas 5 letras representam por volta de 40% da mensagem) e os artigos (no caso da língua portuguesa). Em seguida, tendo identificado alguns casos, podemos partir para identificar as palavras curtas (de 2 a 3 letras). Finalmente, podemos completar a solução utilizando apenas nosso conhecimento linguístico.
Cifra:
TLZQVTVXDQVQHKTLTFZQEQGVRTVKTRTLVRGOLVRGVEXKLGVRTVEGDHXZQEQGVRQVXYKP
Combinações:
| D | 2 | P | 1 | |
| E | 4 | Q | 8 | |
| F | 1 | R | 6 | |
| G | 6 | T | 8 | |
| H | 2 | V | 12 | |
| K | 4 | X | 4 | |
| L | 5 | Y | 1 | |
| O | 1 | Z | 3 |
As letras que não aprecem no mapa tiverem frequência igual à zero.
Pelas regras, podemos assumir que o V representa o espaço. Substituindo temos:
TLZQ T XDQ QHKTLTFZQEQG RT KTRTL RGOL RG EXKLG RT EGDHXZQEQG RQ XYKP
Podemos ver que apenas uma palavra possue uma letra, que é representada por T. Esta é uma forte candidata a ser uma letra “e”, “o” ou “a”. As palavras com 2 letras são “rt” (que aparece duas vezes), “rg” e “rq”. Como sabemos que “t” é uma vogal, podemos concluir que r é a letra “d”. Substituindo temos:
TLZQ T XDQ QHKTLTFZQEQG dT KTdTL dGOL dG EXKLG dT EGDHXZQEQG dQ XYKP
Com isso, podemos aferir que “g” e “q” também são vogais, e, mais ainda, que “t”, “g” e “q” representam “a”, “o” e “e”, não necessariamente nessa ordem. Sabendo disso, podemos analisar o código “EGDHXZQEQG” (sublinhado acima). Sabemos que a palavra termina por duas dessas 3 vogais, com isso, temos altas chances de Q representar “a” e G representar “o”.
Continuando nessa linha de análise chegaríamos no seguinte texto plano:
ESTA E UMA APRESENTACAO DE REDES DOIS DO CURSO DE COMPUTACAO DA UFRJ
Com isso,vemos que, apesar de ser necessário alguns testes, reduzimos bastante o número de testes para que a cifra fosse quebrada. Essa redução já pode ser considerada uma quebra.
Uma cifra de transposição é aquela que, ao contrário da cifra vista anteriormente, não substitui nenhum caractere da mensagem original, apenas “rearruma” esses caracteres de acordo com algum sistema específico, para que, qualquer um que conheça esse sistema, possa ler a mensagem.
Em uma cifra de transposição simples a mensagem é escrita em uma “tabela”, onde o número de colunas se da pela chave, e o número de linhas pelo tamanho da mensagem. A mensagem é, então, escrita linha por linha dentro desta tabela, e removida coluna por coluna em uma ordem determinada pela chave. O tamanho da mensagem deve ser multiplo do tamanho da chave, caso essa condição não seja satisfeita no início, devemos inserir letras aleatórias no final da mensagem até que esta condição seja satisfeita.
Texto Plano: O ATAQUE SERA NO DIA D NA HORA H
Chave: 315243
Criptografia:
| 3 | 1 | 5 | 2 | 4 |
|---|---|---|---|---|
| O | A | T | A | Q |
| U | E | S | E | R |
| A | N | O | D | I |
| A | D | N | A | H |
| O | R | A | H | X |
Com isso, tiramos as letras da tabela linha por linha na ordem indicada pela chave:
AENDR AEDAH OUAAO QRIHX TSONA
Apesar de simples, uma cifra de transposição desse tipo não é fácil de ser quebrada. Através de um mapa de frequência perceberíamos que esta cifra não foi gerada através de substituição e sim através de uma transposição.
A partir do comprimento de cada bloco de caracteres podemos concluir que a chave possui 5 dígitos. Com isso, deveríamos reescrever a mensagem em uma tabela de 5 linhas e 5 colunas:
| A | A | O | Q | T |
| E | E | U | R | S |
| N | D | A | I | O |
| D | A | A | H | N |
| R | H | O | X | A |
Em seguida devemos analisar os pares de letras em cada linha para tentarmos identificar os dígrafos mais comuns na língua portuguesa. Para este próposito existem livros e artigos na internet que listam os dígrafos mais comuns. Por exemplo, na primeira linha temos os dígrafos “ao”, “ta” e “to”. Fazendo isso para todas as linhas encontraríamos os seguintes resultados:
Apesar de ter algumas contradições, podemos extrair alguns padrões do quadro acima:
5-2; 1-5
Tendo essas duas combinações de colunas, conseguiríamos descobrir os outros pares mais frequentes:
3-1; 2-4
Com isso, restaria-nos apenas relizar testes em cima dessas combinações de colunas até o ponto em que as palavras façam sentido linguístico. O que aconteceria quando começassemos pela coluna 3: a cifra RHOXA seria rearranjada em HORAX.
Esse método de encriptação é considerado bastante simples, pois pudemos precisar o tamanho da chave e da cifra apenas olhando para a cifra, o que facilita bastante a quebra deste tipo de cifra.
Vale ressaltar mais uma vez que a quebra dessa cifra se deu com um número de passos relativamente pequeno, devido à simplicidade da cifra. Cifras de subsituição mais complexas necessitam de um número muito maior de passos do que os aqui realizados, mas ainda assim este número é muito inferior ao da quebra pelo método da força bruta.
O ataque do aniversário é um ataque criptográfico que difere dos vistos anteriormente pelo fato de ser baseado na força bruta. Ele utiliza as premissas encontradas no Problema do Aniversário, que consistem na probabilidade de, numa coleção randômica de n pessoas, duas pessoas fazerem aniversário no mesmo dia. Resolvendo este problema chegamos na seguinte probabilidade de que, quando temos n pessoas na distribuição, existirá ao menos uma colisão nas datas de aniversário:

Pela tabela acima, podemos ver que para 23 pessoas na amostra a probabilidade de que ao menos 2 façam aniversário na mesma data é de 50%. Modificando o conceito para um ataque, podemos usar este problema para explorar a resistência a colisão de uma função hash, que diz que, dada uma função de hash h, para qualquer par (x, y) deve ser impossível encontrar h(x) = h(y). Estendo um pouco essa idéia, podemos enunciar o seguinte problema: dado uma função de hash com n possibilidades de endereçamento e um número k de mensagens que chegam a essa função, qual o valor mínimo de k para que pelo menos duas mensagens tenham a mesma função de hash? No Problema do Aniversário temos que n = 365.
A probilidade do evento acima ocorrer é igual a P(n, k) = 1 – P(A’), onde A’ é a probabilidade de nenhuma das mensagens terem a mesma função hash. Subsituindo as variáveis do problema descrito acima no problema do aniversário temos que P vale:
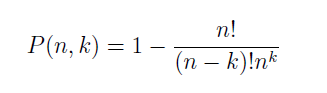
Usando a desigualdade (1-x) < e-x chegamos a:
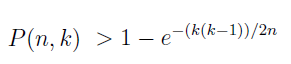
Calculando para que essa probabilidade seja 50%:
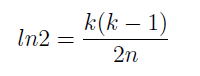
O que para um valor de k muito grande:
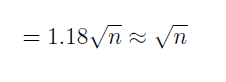
Com isso, se cada mensagem tem m bits, logo a tabela hash tem 2m entradas, e para que uma mensagem seja falsificada baste que o intruso teste k = 2m/2 mensagens diferentes. Com isso, este teria 50% de chance de validar uma mensagem falsa.